In this article, we'll explore and understand how compound interest works and how it can help our investments grow faster and really make a big difference. It is a great technique to use when saving or investing for the longer term.

Terms

Compound interest is one of the ways that interest gets added to an investment. (The other method of calculating interest is called simple interest.)

How Does Compounding Work?

Let us say that we deposit our money in a bank account that provides compound interest. Every year some interest is added to the principal amount — this yearly period is called the compounding period. The amount of interest that $100 can earn in a year is called the rate of return of that investment.

Note: the compounding period (how often interest gets added) could be quarterly, semi-annual, monthly, or yearly. Different investments and loans adopt different different compounding periods. In this article, we'll assume yearly compounding for ease of understanding. The mechanism of compounding is the same irrespective of the compounding period.

The First Year

At the end of the first year, the interest accrued during the year gets added to our principal, and thus the amount at the end of the year is principal + interest. This is true for both simple and compound interest. Thus, for year one, there isn't any difference between simple and compound interests.

Subsequent Years

At beginning of year two, things start to differ between simple and compound interests. In the case of simple interest, the interest gained in year one is set aside, and the principal for year two is the same as the principal for year one. In the case of compound interest, the final amount of year one (principal + interest) now becomes the principal for the second year!

Thus, in the second year, the simple interest will once again be the same amount as it was in year one. In the case of compound interest, the interest is calculated for the now slightly bigger principal amount and thus will be a little bit more than that in year one.

It doesn't stop there. Starting from the second year, this "interest of this year getting added to principal for next year" happens every year in the case of compound interest. Thus, every year's principal will be more than the previous year's principal and therefore, so will be the interest earned that year. We can easily imagine how this can add up to a significant increase over several years.

This is the magic of compounding.

Contrast this with simple interest: in the case of simple interest, because the interest gained in the previous year is set aside and only the original principal is considered when calculating this year's interest, every year's interest remains the same.

Example

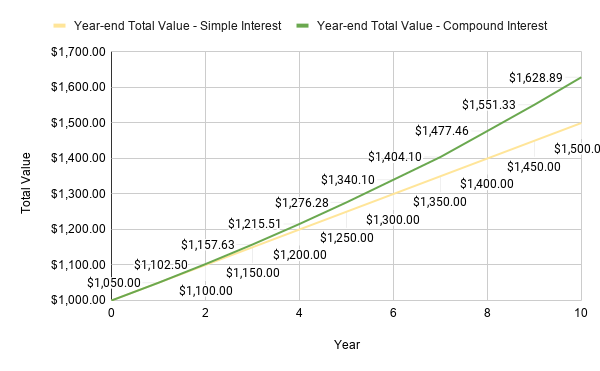
Let's see how the same principal amount grows with simple interest and with compounding, using a sample principal of $1000.00 invested at a rate of return of 5.0% per year for 10 years.

Starting principal: $1000.00
Annual rate of return: 5.00%
Number of years: 10

The "Annual Interest" column shows the interest accrued every year. And, the last column shows the current value of the investment at the end of each year.

Year	Interest Type	Year-start Principal	Annual Interest	Year-end Value
1	Simple	$1000.00	$50.00	$1050.00
	Compound	$1000.00	$50.00	$1050.00
2	Simple	$1000.00	$50.00	$1100.00
	Compound	$1050.00	$52.50	$1102.50

Notice that in the first year, both simple and compound interests yield the same interest ($50). In the second year, the interest with compounding (and therefore the year-end investment value) is already (slightly) bigger than with simple interest. In fact, this trend will continue — from now onwards, though the simple interest every year will remain the same ($50), compounding will always yield higher interest every year than the simple interest. Let's continue:

Year	Interest Type	Year-start Principal	Annual Interest	Year-end Value
3	Simple	$1000.00	$50.00	$1150.00
	Compound	$1102.50	$55.13	$1157.63
4	Simple	$1000.00	$50.00	$1200.00
	Compound	$1157.63	$57.88	$1215.51
5	Simple	$1000.00	$50.00	$1250.00
	Compound	$1215.51	$60.78	$1276.28
6	Simple	$1000.00	$50.00	$1300.00
	Compound	$1276.28	$63.81	$1340.10
7	Simple	$1000.00	$50.00	$1350.00
	Compound	$1340.10	$67.00	$1407.10
8	Simple	$1000.00	$50.00	$1400.00
	Compound	$1407.10	$70.36	$1477.46
9	Simple	$1000.00	$50.00	$1450.00
	Compound	$1477.46	$73.87	$1551.33
10	Simple	$1000.00	$50.00	$1500.00
	Compound	$1551.33	$77.57	$1628.89

At the end of 10 years:

Interest Type	Total Interest Earned	Total Value	Gain Percent
Simple	$500.00	$1500.00	(500 / 1000) x 100 = 50%
Compound	$628.89	$1628.89	(628.89 / 1000) x 100 = 62.89

In other words, compound interest provided an additional 12.89% percent boost (62.89 − 50) to our principal in 10 years. See "Compounding Catalysts" below for factors that could increase this gain even more.

The same information is shown in the graph below. We can see how compounding results in a much bigger return in 10 years.

Compounding Catalysts

What are the things that help increase the investment's worth over time?

• Bigger principal — Needless to say, the bigger the principal, the bigger the interest amount. For the same rate of return of, say, 5% a year, a principal of $1000 will yield an interest of $50 in the first year, whereas a principal of $2000 will fetch an interest of $100 in the first year. Because the first year's principal and interest together make up the second year's principal, the second year's principal now becomes $1050 and $1100, respectively.
• Higher rate of return — A higher rate of return results in a bigger interest amount, boosting the next year's principal.
• Longer time frame — This is where compounding shines. As time goes by, the increase in principal itself becomes bigger every year.

Investment Examples

Typical investments that use simple interest to calculate interest are:

• Government Bonds (e.g., US Treasury bills, local municipal bonds).
• Corporate Bonds — Companies borrow money from us, for which we are paid an interest periodically.

Typical investments that calculate interest using compounding are:

• Bank accounts
• Mutual funds
• Annuities

Considerations

There are a few things we need to keep in mind about compounding and, more importantly, about the different types of compounding investments that banks, mutual funds, annuities, etc., offer:

• Compounding takes time. This is both the biggest advantage and disadvantage. This makes investing in a compounding fund a good choice for a long-term investment, where we don't need the earned interest right away (or every year).
• Some investments (such as bank accounts, some mutual funds) may cause us to pay a tax every year on the interest/gain earned during that year, even if we didn't withdraw any money from the investment. In contrast, some other investments allow the interest to grow tax-free until we're ready to withdraw any money — we need to pay taxes on the profit only when we withdraw.
• Some compoundng schemes require a minimum principal amount.
• Some schemes may also charge an annual operating fee. Sometimes the fee is waived if the principal amount is sufficiently large, as decided by the investment company.

It is always a good idea to consult with a competent financial advisor and a tax consultant to understand these nuances when investing.

Doubling Rule

There's a simple rule called the doubling rule or rule of 72 that lets us quickly calculate a) the interest rate required to double the value of the principal in a given time period, or b) given an investment's interest rate, how long to invest for the investment to double in value:

• Rate of return = 72 / #years. For example, if we're investing for 10 years and want our principal to double in value, we need to select an investment that has a compound interest rate of 72/10, that is 7.2%, per year.
• The reverse is also true: #years to double in value = 72 / rate of return. If an investment offers a compounding interest of, say, 5% per year, our money will double in about 14 (72/5 = 14.4) years.

Summary

We learnt what compounding is and how it compares with simple interest. We saw how the principal amount, time frame and rate of return can influence the growth. We also touched upon things to think about when investing in an investment offering compound interest.

Armed with this information, you should now be able to talk to your financial advisor to select the right kind of compounding investment for your needs.